目的:
麻雀の「実力」を試合結果だけから評価するのは簡単ではない。
例えばリーチ勝負で、どちらが先に相手の当たり牌をつかむか、で、1位になるか4位になるかが決まったりする。
「長い目で見れば~~した方が勝てる」などと言われるが、実際どの程度「長い目」で見ればよいのかさえ理解されていないのが現状だろうと推察する。
打つところを後ろから見ていれば、だいたいの「強さ」はわかるような気もするのだが、どうも見る人の好みや打ち方によって評価はまちまちになるし、なにより定量化できる方法ではないだろう。
「最近の試合の平均順位」から実力を評価するのは、シンプルだが非常に客観的で、合理的で、信頼できる方法の一つである。
ここでは、試合数・順位分布による平均順位の偏りの度合いを定量化し、ある信頼度で実力を計測したい場合に必要な試合数を求める計算方法などを紹介する。
なお、実力の計測という課題は、麻雀研究の全ての基礎となる。研究を志す者は、以下について熟知しておくべきである。
理論計算:
1試合あたりでj位をとる確率がP(j)であるプレイヤーを考える。
平均順位J=ΣiP(i)である。
(なおここでは、Σはi=1~4を表すものとする)
1試合終了時の順位の分散はΣP(i)・(i-J)^2だから、n試合終了時の順位合計の分散は
nΣP(i)・(i-J)^2
と書ける。
一般にn試合終了時平均順位の、「真の平均順位」からの変化分の標準偏差σは
σ = √{A/n}
ただしA=ΣP(i)(i-J)^2、一般的にはA=1.25弱
と表せる。
P(j):1試合あたりでj位になる確率、J:1試合あたりの平均順位、n:試合数
なお、安定Rの変化分で表示すると
σ(R) = 1200 × √{A/n}
ただしP(j):1試合あたりでj位になる確率、J:1試合あたりの平均順位、n:試合数
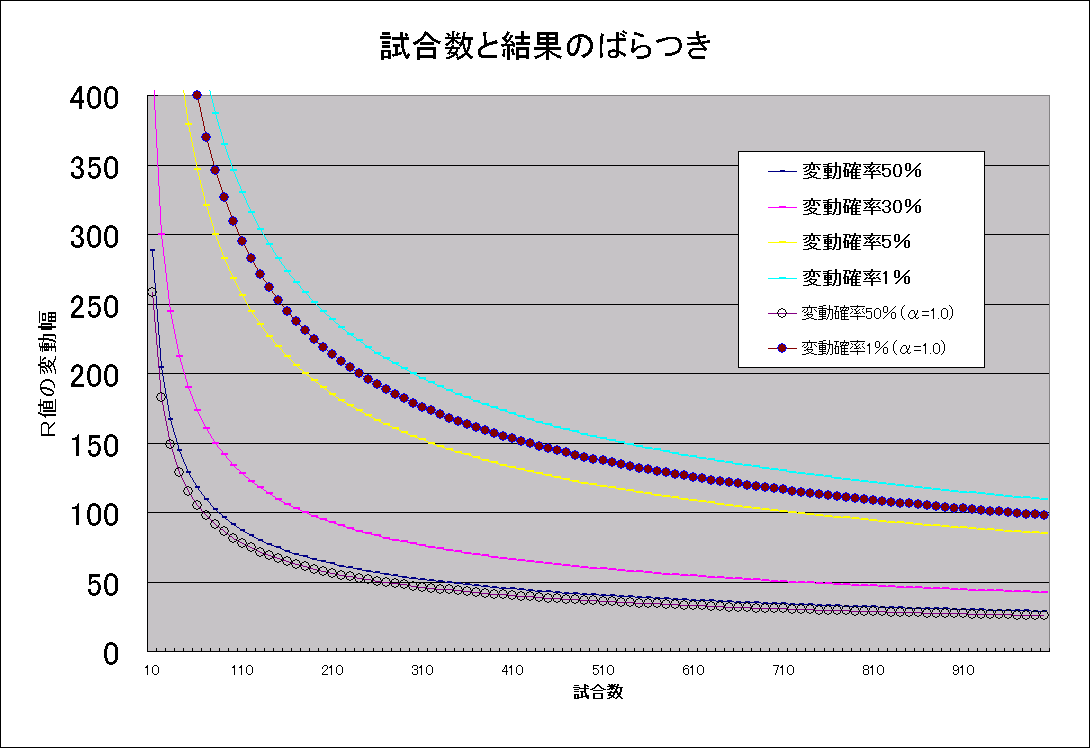
下図は、A=1.25の場合と、A=1.00の場合の一部の、試合数と結果の変動関係を、各々の信頼度でグラフにプロットしたものである。
図1:試合数と結果のばらつき(A=1.25,A=1.00)
A値について:
A値は、「(順位分布の特徴による)成績のばらつきやすさの指標」であると言うことができる。
今後A値は「順位分布係数」「偏りのA」などと呼ばれることがある。
成績(平均順位)の分散は、順位分布係数Aに比例し、試合数nに反比例する。
仮に、P(1~4)=0.25、つまり1位2位3位4位すべて、25%の確率でとるプレイヤーを考えると、
A=ΣP(i)・(i-J)^2=5/4だから、
1~4位を等しく取るプレイヤーの、n試合終了時平均順位の「真の平均順位」からの変化分の標準偏差σは
σ = √{1.25/n}
n:試合数
となる。
安定R表記では
σ(R) = 1200×√{1.25/n}
n:試合数
である。
平均的なプレイヤーのAは1.25であるのに対して、P(1)=0.3、P(2)=0.27、P(3)=0.23、P(4)=0.2、平均順位2.33の「勝ち組」の人のAはどうだろうか。
A=0.3*(1-2.33)^2+0.27*(2-2.33)^2+0.23*(3-2.33)^2+0.2*(4-2.33)^2=1.2211
と計算でき、
σ(R) = 1200 × √{1.2211/n}
となる。
P(1)=0.3、P(2)=0.2、P(3)=0.2、P(4)=0.3、平均順位2.5の「かなり極端な打ち手」のAが、1.45となった。
Aの値はこのようにおおむね1.2~1.45前後の値であり、平均順位のばらつきは順位分布の変化にはあまり依存しないことがわかる。
普通、順位分布は上記に示したような「現実的な」値を取るから、通常は 1.2≦A≦1.45 程度についてだけ考えれば充分である。
ただしこの方法は、必ずしも「~~試合の中からよかったn試合を取り出す」場合の平均順位のばらつきを計算するのに適した方法ではない。そのような場合は別の議論が必要である。
A値の変化(および最大値と最小値)に関する補題:(やや難解。普通の読者は飛ばしてください)
P(1)=x、P(2)=y、P(3)=zとすると(ただし0<=x<=1、0<=y<=1、0<=z<=1、0<=x+y+z<=1)、平均順位J=x+2y+3z+4(1-x-y-z)と表すことができ、
A = x{x+2y+3z+4(1-x-y-z)-1}^2+y{x+2y+3z+4(1-x-y-z)-2}^2+z{x+2y+3z+4(1-x-y-z)-3}^2+(1-x-y-z){x+2y+3z+4(1-x-y-z)}^2
のように表現できるが、これを気合で展開すると、
A = 9x(1-x)+4y(1-y)+z(1-z)-12xy-6xz-4yz
= -(3x+2y+z)^2+9x+4y+z
ときれいに展開できる(ハァハァ)。
Aの、最大値と最小値を求めよう。
まずは簡単のために1位と4位のみを取る場合、つまりP(1)=x、P(2)=y=0、P(3)=z=0と置くときを考えると、
A=9x(1-x)=-9x^2+9x
より
dA/dx = -18x+9
から、x=0.5においてAは最大値2.25を取ることがわかる。
これをあらゆる可能な順位分布に一般化する。
A=9/4-2y-2z-(3x+2y+z-3/2)^2
と変形すると、明らかに
A<9/4
等号成立はy=z=0かつ3x+2y+z-3/2=0の時である。
以上より、Aの最大値となる順位分布は
P(1)=x=0.5、P(2)=y=0、P(3)=z=0、P(4)=1-x-y-z=0.5
であり、そのときのAの値は2.25であることが証明された。
逆に最小値について考えると、特定の順位のみを取り続ける場合に限ってAは最小となり、A=0となる。これは自明である。
<参考>
x+y+z=k、x+y=mとして
∂A(x,m,k)/∂x=-2x-2m-2k+5
∂A(x,m,k)/∂m=-2x-2m-2k+3
∂A(x,m,k)/∂k=-2x-2m-2k+1
dA = {∂A(x,m,k)/∂x}dx+{∂A(x,m,k)/∂m}dm+{∂A(x,m,k)/∂k}dk
dA = (-2x-2m-2k+5)dx+(-2x-2m-2k+3)dm+(-2x-2m-2k+1)dk
これらの式から、Aの変化のしかたを、実際にAを計算することなく簡単に把握できる。
例えば「トップ率を少し増やし、4位率をそれと同じだけ減らし、2位率と3位率とを一定に保つ場合」だと、dm=dk=dxとするので、
dA = (-2x-2m-2k+5)dx+(-2x-2m-2k+3)dx+(-2x-2m-2k+1)dx
= (-6x-6m-6k+9)dx
を考えれば良い。
トップ率0.5、2位率0、3位率0の場合、つまりx=0.5,m=0.5,k=0.5の近傍において、トップ率と4位率だけを、微小なeだけ変化させる場合の挙動を考えよう。
トップ率0.5+e、2位率0、3位率0の場合、x=0.5+e、m=0.5+e、k=0.5+eとなり、dA = -18e
「y=0,z=0という条件下での、x=0.5の近傍においては」次のような増減表が描ける。